AlgeoMath | 알지오매스

로그인

고등학교[함수의 그래프] 두 그래프의 교점의 개수

주제 확인하기: 이차함수 $y=ax^2+bx+c$ 와 일차함수 $y=mx+n$ 의 교점의 개수를 구해보세요.

이차함수의 그래프와 직선의 위치 관계
이차함수 $y=ax^2+bx+c$ 의 그래프와 직선 $y=mx+n$ 의 교점의 $x$ 좌표는 이차방정식 $ax^2+bx+c=mx+n$ ,

즉 $ax^2+(b-m)x+(c-n)=0$ $\; \cdots \, \cdots \;$ ⓛ
의 실근과 같다.

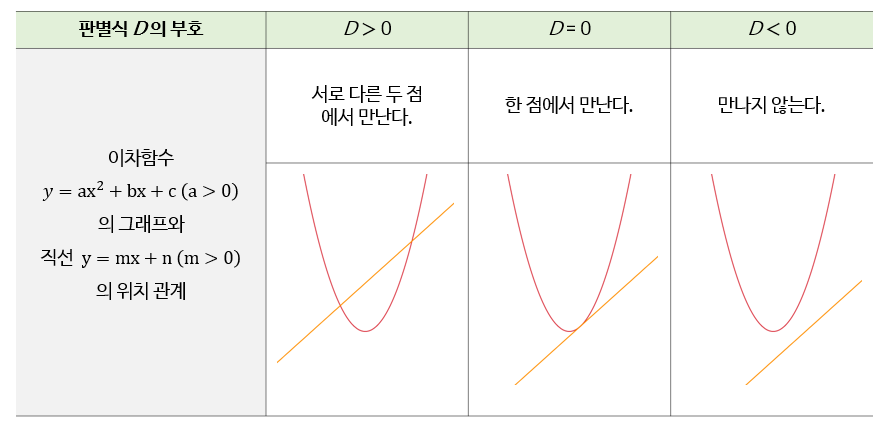
따라서 이차함수의 그래프와 직선의 교점의 개수는 이차방정식 ①의 실근의 개수와 같고, 이차방정식 ①의 판별식 $D$ 의 부호에 따라 이차함수의 그래프와 직선의 위치 관계는 다음과 같다.

1. 주제 해결 영상을 보면서 각 핵심 기능들을 살펴보세요.

해결 영상 미리보기

핵심 기능 살펴보기

대수입력

수식을 입력하여 간단한 계산이나 점, 그래프 등을 그릴 수 있습니다.

슬라이더

평면상에 슬라이더를 생성하는 기능입니다. 생성된 슬라이더는 대수창에도 표현되며 대수를 입력할 때 변수로 사용할 수 있습니다.

교점

평면상에 두 객체의 교점을 생성하는 기능입니다. 교점을 생성할 두 대상을 선택하세요.

2. 단계별로 주어진 미션을 아래 실습창에서 해결해 보세요.

미션 수행하기

Step 1. 이차함수 $y=f(x)$ 그리기(1): 대수창에 『 y=ax^2+bx+c 』 을 입력하세요.

Step 1. 이차함수 $y=f(x)$ 그리기(2): 슬라이더를 조작하여 $a$ , $b$ , $c$ 의 값을 조정하면서 이차함수의 모양을 살펴보세요.

Step 2. 일차함수 $y=g(x)$ 그리기(1): 대수창에 『 y=mx+n 』 을 입력하세요.

Step 2. 일차함수 $y=g(x)$ 그리기(2): 슬라이더를 조작하여 $m$ , $n$ 의 값을 조정하면서 일차함수의 모양을 살피고 두 그래프가 겹치게 놓아보세요.

Step 3. 이차함수 $y=f(x)$ 와 일차함수 $y=g(x)$ 의 교점 구하기: 알지오매스 교점 기능으로 두 그래프의 교점을 찾아보세요.

Step 4. $f(x)-g(x)=0$ 의 판별식 $D$ 의 값에 따른 교점의 개수 비교하기(1): 대수창에 판별식 의 값인 『 (b-m)^2-4a(c-n) 』 을 입력하세요.

Step 4. $f(x)-g(x)=0$ 의 판별식 $D$ 의 값에 따른 교점의 개수 비교하기(2): 두 그래프간에 1개 이상의 교점이 만들어지기 위해서는 판별식 $D$ 의 값이 어떻게 정해져야 하나요?

3. 샘플을 확인하면서 실습한 내용을 다시 한 번 확인해 보세요.

샘플 확인하기