검색

고등학교[벡터의 연산] 두 벡터의 합과 차

주제 확인하기
두 벡터 a⃗=(1,2)\vec{a}=(1,2) 와 b⃗=(3,1)\vec{b}=(3,1) 의 합과 차를 각각 구해보세요.

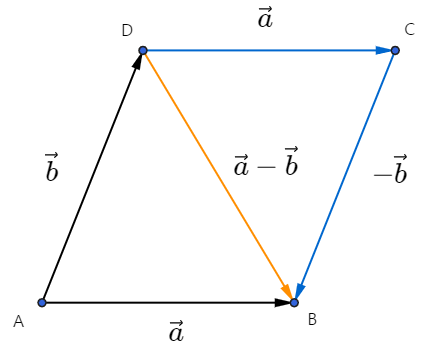
두 벡터의 합과 차

두 벡터 a⃗\vec{a} , b⃗\vec{b} 에 대하여 a⃗=AB→\vec{a}=\overrightarrow{AB} , b⃗=BC→\vec{b}=\overrightarrow{BC} 가 되도록 세 점 AA , BB , CC 를 잡을 때, AC→\overrightarrow{AC} 를 두 벡터 a⃗\vec{a} 와 b⃗\vec{b} 의 합이라 하며, 이것을 기호로 나타내면 a⃗+b⃗\vec{a}+\vec{b} 와 같다.

그리고 a⃗=AB→\vec{a}=\overrightarrow{AB} , b⃗=AD→\vec{b}=\overrightarrow{AD} 가 되도록 세 점 AA , BB , DD 를 잡고, 사각형 ABCDABCD 가 평행사변형이 되도록 점 CC 를 잡으면
a⃗−b⃗\vec{a}-\vec{b} =a⃗+(−b⃗)=AB→+(−AD→)=DC→+CB→=DB→=\vec{a}+(-\vec{b})=\overrightarrow{AB}+(-\overrightarrow{AD})=\overrightarrow{DC}+\overrightarrow{CB}=\overrightarrow{DB} 이다.

1. 주제 해결 영상을 보면서 각 핵심 기능들을 살펴보세요.

해결 영상 미리보기
핵심 기능 살펴보기
텍스트
텍스트텍스트

평면상에 텍스트를 생성하는 기능입니다. 텍스트를 입력할 위치를 선택하세요.

벡터
벡터벡터

평면상에 벡터를 생성하는 기능입니다.

점대칭
점대칭점대칭

주어진 도형이 선택한 기준점을 중심으로 대칭 이동되어 생성됩니다. 관련된 대상을 삭제하면 대칭된 도형도 같이 삭제됩니다.

평행이동
평행이동평행이동

대상의 모양과 크기를 바꾸지 않고 일정한 방향으로 일정한 거리만큼 옮길 수 있습니다. 평행이동에 의해 만들어진 벡터의 점을 이동시켜 벡터의 값을 변경시키면 변경된 내용이 대상에도 적용됩니다.

2. 단계별로 주어진 미션을 아래 실습창에서 해결해 보세요.

미션 수행하기
튜토리얼 아이콘
Step 1. 벡터 a⃗\vec{a} , b⃗\vec{b} 그리기(1)
시점이 (0,0)(0,0) 이고 종점이 (1,2)(1,2) 인 벡터 a⃗\vec{a} 를 그리세요.
[도움영상]
튜토리얼 아이콘
Step 1. 벡터 a⃗\vec{a} , b⃗\vec{b} 그리기(2)
시점이 (0,0)(0,0) 이고 종점이 (3,1)(3,1) 인 벡터 b⃗\vec{b} 를 그리세요.
[도움영상]
튜토리얼 아이콘
Step 1. 벡터 a⃗\vec{a} , b⃗\vec{b} 그리기(3)
알지오매스 텍스트 기능을 이용하여 벡터 a⃗\vec{a} 근처에 『 \vec{a} 』를 입력하고 LaTeX을 체크하세요.
[도움영상]
튜토리얼 아이콘
Step 1. 벡터 a⃗\vec{a} , b⃗\vec{b} 그리기(4)
알지오매스 텍스트 기능을 이용하여 벡터 b⃗\vec{b} 근처에 『 \vec{b} 』를 입력하고 LaTeX을 체크하세요.
[도움영상]
튜토리얼 아이콘
Step 2. 벡터 a⃗+b⃗\vec{a}+\vec{b} 그리기(1)
벡터 a⃗\vec{a} 의 종점 BB 를 벡터 b⃗\vec{b} 만큼 평행이동 시켜 벡터 a⃗+b⃗\vec{a}+\vec{b} 의 종점 DD 를 그리세요.
[도움영상]
튜토리얼 아이콘
Step 2. 벡터 a⃗+b⃗\vec{a}+\vec{b} 그리기(2)
벡터 a⃗\vec{a} 의 시점인 점 AA 와 벡터 a⃗+b⃗\vec{a}+\vec{b} 의 종점인 점 DD 를 잇는 벡터 a⃗+b⃗\vec{a}+\vec{b} 를 그리세요.
[도움영상]
튜토리얼 아이콘
Step 2. 벡터 a⃗+b⃗\vec{a}+\vec{b} 그리기(3)
알지오매스 텍스트 기능을 이용하여 벡터 a⃗+b⃗\vec{a}+\vec{b} 근처에 『 \vec{a}+\vec{b} 』를 입력하고 LaTeX을 체크하세요.
[도움영상]
튜토리얼 아이콘
Step 3. 벡터 −b⃗-\vec{b} 그리기(1)
벡터 b⃗\vec{b} 의 종점 CC 를 시점인 점 AA 를 기준으로 점대칭 이동시키세요.
[도움영상]
튜토리얼 아이콘
Step 3. 벡터 −b⃗-\vec{b} 그리기(2)
벡터 b⃗\vec{b} 의 시점인 점 AA 와 벡터 −b⃗-\vec{b} 의 종점인 점 EE 를 잇는 벡터 −b⃗-\vec{b} 를 그리세요.
[도움영상]
튜토리얼 아이콘
Step 3. 벡터 −b⃗-\vec{b} 그리기(3)
알지오매스 텍스트 기능을 이용하여 벡터 −b⃗-\vec{b} 근처에 『 -\vec{b} 』를 입력하고 LaTeX을 체크하세요.
[도움영상]
튜토리얼 아이콘
Step 4. 벡터 a⃗−b⃗\vec{a}-\vec{b} 그리기(1)
벡터 a⃗\vec{a} 의 종점 BB 를 벡터 −b⃗-\vec{b} 만큼 평행이동 시켜 벡터 a⃗−b⃗\vec{a}-\vec{b} 의 종점 GG 를 그리세요.
[도움영상]
튜토리얼 아이콘
Step 4. 벡터 a⃗−b⃗\vec{a}-\vec{b} 그리기(2)
벡터 a⃗\vec{a} 의 시점인 점 AA 와 벡터 a⃗−b⃗\vec{a}-\vec{b} 의 종점인 점 GG 를 잇는 벡터 a⃗−b⃗\vec{a}-\vec{b} 를 그리세요.
[도움영상]
튜토리얼 아이콘
Step 4. 벡터 a⃗−b⃗\vec{a}-\vec{b} 그리기(3)
알지오매스 텍스트 기능을 이용하여 벡터 a⃗−b⃗\vec{a}-\vec{b} 근처에 『 \vec{a} -\vec{b} 』를 입력하고 LaTeX을 체크하세요.
[도움영상]
튜토리얼 아이콘
Step 5. 벡터 a⃗\vec{a} , b⃗\vec{b} 와 벡터 a⃗+b⃗\vec{a}+\vec{b} , a⃗−b⃗\vec{a}-\vec{b} 의 관계 살펴보기
벡터 a⃗\vec{a} , b⃗\vec{b} 를 조정하여 변화된 벡터 a⃗+b⃗\vec{a}+\vec{b} , a⃗−b⃗\vec{a}-\vec{b} 를 살펴보세요. 서로 어떤 관계가 있나요?
[도움영상]

3. 샘플을 확인하면서 실습한 내용을 다시 한 번 확인해 보세요.

샘플 확인하기
AlgeoMath Team

(06130) 서울시 강남구 테헤란로 7길 22(역삼동, 과학기술회관 2관) 한국과학창의재단(4층~5층)전화 02-555-0701팩스 02-555-0702

Copyright © KOSAC. All rights reserved.